Question 1:
A. State the null and alternative hypothesis
Null Hypothesis (H₀):
The mean breaking strength of cookies produced by the new machine is equal to the specified mean of 70 pounds.
H0 : μ = 70
Alternative Hypothesis (H₁):
The mean breaking strength of cookies produced by the new machine is different from the specified mean of 70 pounds.
H1 : μ ≠ 70
B. Is there evidence that the machine is not meeting the manufacturer’s specifications for average strength? Use a 0.05 level of significance

This code shows that the null hypothesis cannot be rejected because the calculated z-score falls within the range of the critical z-values, indicating that there is not enough evidence to suggest that the machine’s mean cookie strength significantly differs from the manufacturer’s specified mean.
C. Compute the p value and interpret its meaning

The p-value is approximately 0.0719. The p-value represents the probability of obtaining a test statistic at least as extreme as the one observed (in this case, a z-score of approximately -1.80), assuming the null hypothesis is true. Since the p-value (0.0719) is greater than the significance level (α=0.05), we do not have enough evidence to reject the null hypothesis. If the p-value was less than 0.05 (the significance level), it would indicate that the observed data is statistically significant, meaning the likelihood of obtaining the observed result, assuming the null hypothesis is true, is very low.
D . What would be your answer in (B) if the standard deviation were specified as 1.75 pounds?

This code shows that the null hypothesis should be rejected because the calculated z-score falls outside the range of the critical z-values, indicating that there is evidence to suggest that the machine’s mean cookie strength significantly differs from the manufacturer’s specified mean.
E. What would be your answer in (B) if the sample mean were 69 pounds and the standard deviation is 3.5 pounds?
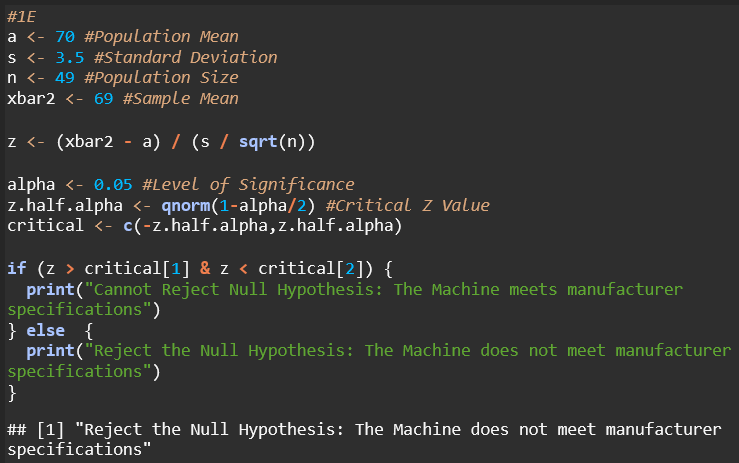
This code shows that the null hypothesis should be rejected because the calculated z-score falls outside the range of the critical z-values, indicating that there is evidence to suggest that the machine’s mean cookie strength significantly differs from the manufacturer’s specified mean.
Question 2:
If x̅ = 85, σ = standard deviation = 8, and n=64, set up 95% confidence interval estimate of the population mean μ.

Question 3:
Data Manipulation and Munging:
A. Calculate the correlation coefficient for this data set
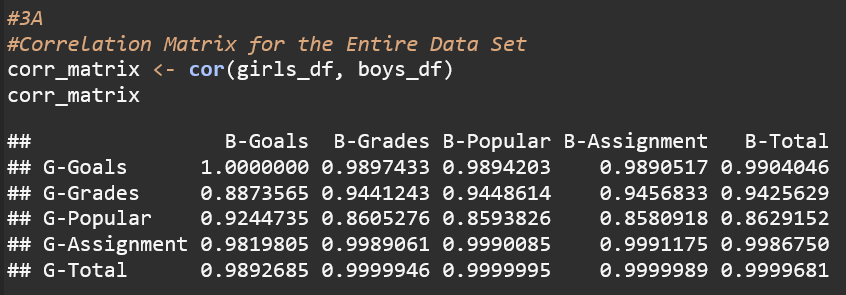
B. Pearson correlation coefficient for x= girls and y =boys. (goals, time spend on assignment)

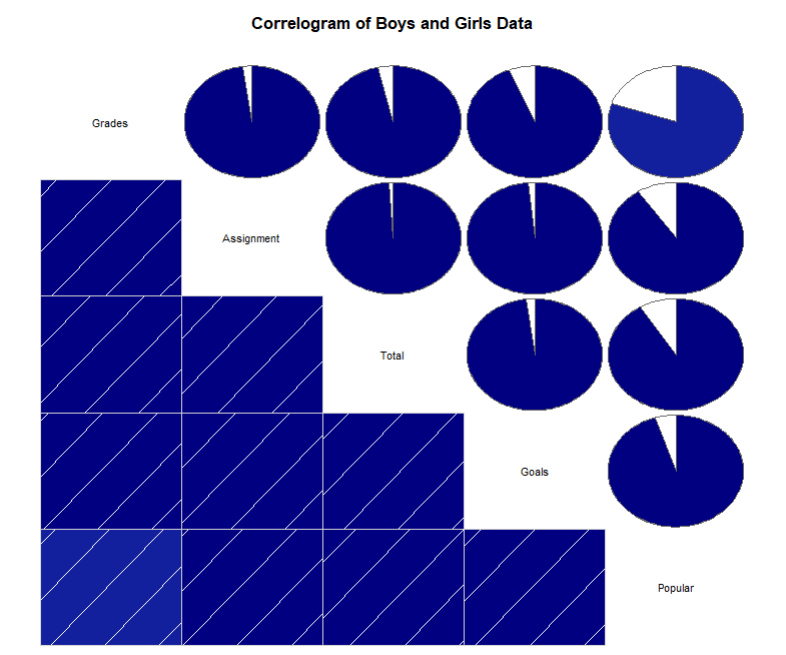
C. Create plot of the correlation

Leave a comment